MABS Institution
9th Mathematics Model Exam -1-Aug 2020
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Represent the following sets in Roster form.
A = The set of all even natural numbers less than 20. -
Factorise the following: a3+3a2b+3ab2+2b3
-
You are walking along a street. If you just choose a stranger crossing you, what is the probability that his next birthday will fall on a sunday?
-
Write the following in scientific notation: (50000000)4
-
Twice the area of a right angled triangle 15x2 + 19x + 6 sq. units. If its altitude is 5x + 3 units, find its base in terms of x.
-
Determine whether (x -1) is a factor of the following polynomials: x4+5x2-5x+1
-
In a survey of 400 youngsters aged 16-20 years, it was found that 191 have their voter ID card. If a youngster is selected at random, find the probability that the youngster does not have their voter ID card.
-
IfA= {1,2,3} B= {3,5,6} C={3,4,7}.Find(i)A-(BUC) (ii) BΔC (iii)AΔB
-
Check whether \(\frac { 1 }{ 4 } \) is a solution of the equation 3(x + 1) = 3( 5–x) – 2( 5 + x).
-
Express the following in the form \({p\over q},\) where p and q are integers and q \(\ne\) 0.
\(0.\overline {47}\) -
Express the following in the form \({p\over q},\) where p and q are integers and q \(\ne\) 0.
\(0.5\overline {7}\) -
Simplify: (2.75 x 107)+(1.23 x 108)
-
In a class of 50 students, each one come to school by bus or by bicycle or on foot. 25 by bus, 20 by bicycle, 30 on foot and 10 students by all the three. Now how many students come to school exactly by two modes of transport?
-
Consider the given pairs of triangles and say whether each pair is that of congruent triangles. If the triangles are congruent, say ‘how’; if they are not congruent say ‘why’ and also say if a small modification would make them congruent:
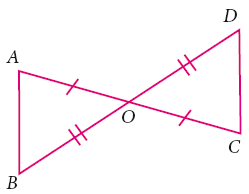
-
Factorise 4r + 2x - 12
-
If the quotient obtained on dividing (8x4-2x2+6x-7) is (4x3+px2-qx+3), then find p, q and also the remainder
-
If \(\left( y-\frac { 1 }{ y } \right) ^{ 3 }\)=27, then find the value of \({ y }^{ 3 }-\frac { 1 }{ { y }^{ 3 } } \) .
-
The average mark of 25 students was found to be 78.4. Later on, it was found that score of 96 was misread as 69. Find the correct mean of the marks
-
Your friend draws a figure such as this on a piece of paper.
You don't know what it is, and stand at the board. She has to describe the figure to you so that you draw exactly the same figure on the board.
You both know rectangles, so it is easy to describe and draw a rectangle. The rest are not easy.
Can we describe any such shape we can ever think of, in a way that another person
hearing it can reproduce it exactly?
Yes, yes, yes! Now, isn't that exciting? The answer is so simple that it is breathtaking.
We describe different shapes by their properties. -
Find the TSA and LSA of a cuboid whose length, breadth and height are 7.5 m, 3 m and 5 m respectively.
-
Rewrite the following polynomial in standard form.
\(\sqrt { 2 } x^{ 2 }-\frac { 7 }{ 2 } { x }^{ 4 }+x-5{ x }^{ 3 }\) -
Express the following decimal expression into rational numbers \(3.1\overline { 7 } \)
-
If A={y:y=\(\frac { a+1 }{ 2 } \), a \(\in \) W and a≤5}, B={y:y=\(\frac { 2n-1 }{ 2 } \), n\(\in \)W and n<5} and C=\(\left\{ -1,-\frac { 1 }{ 2 } ,1,\frac { 3 }{ 2 } ,2 \right\} \), then show that \(A-(B\cup C)=(A-B)\cap (A-C)\).
-
The base of a parallelogram is (5x+4). Find its height, if the area is 25x2–16.
-
A survey of 1000 farmers found that 600 grew paddy, 350 grew ragi, 280 grew corn, 120 grew paddy and ragi, 100 grew ragi and corn, 80 grew paddy and corn. If each farmer grew atleast any one of the above three, then find the number of farmers who grew all the three.
-
-
If A, Band C are overlapping sets, draw venn diagram for:\(A\cap B\)
-
Add the following polynomials and find the degree of the resultant polynomial.
Sl.No Polynomial Addition Degree of the resultant polynomial 1 p(x) = 5x3 - 3x + x2 + 4
q(x) = 7x - 4x2 + 22 p(m) = 6m - 7
q(m) = 7m2 - 12 + 4m3 p(x) = 4x2 - 6x3 - 4x + 6
q(x) = 8x3 + 2x2 - 24 r(y) = 7y4 + 5y2 + 4y
s(y) = 2y - 3y25 p(m) = 12m3 - 10m2 - 7
q(m) = 7m3 + 5m2 - 3
-
-
A and B are two sets such that n(A – B) = 32 + x, n(B – A) = 5x and n(A∩B) = x. Illustrate the information by means of a Venn diagram. Given that n(A) = n(B), calculate the value of x.
