St. Britto Hr. Sec. School - Madurai
12th Maths Monthly Test - 3 ( Two Dimensional Analytical Geometry-II)-Aug 2020
-
-
-
-
-
-
-
-
-
Find the general equation of the circle whose diameter is the line segment joining the points (−4,−2)and (1,1).
-
The line 3x+4y−12 = 0 meets the coordinate axes at A and B . Find the equation of the circle drawn on AB as diameter.
-
Cross section of a Nuclear cooling tower is in the shape of a hyperbola with equation\(\frac { { x }^{ 2 } }{ { 30 }^{ 2 } } -\frac { { y }^{ 2 } }{ { 44 }^{ 2 } } =1\) The tower is 150m tall and the distance from the top of the tower to the centre of the hyperbola is half the distance from the base of the tower to the centre of the hyperbola. Find the diameter of the top and base of the tower.
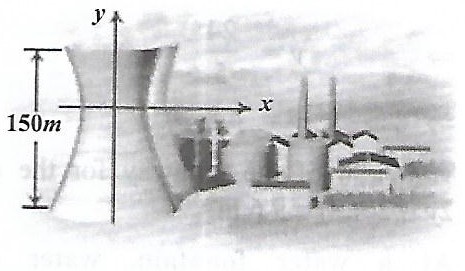
-
Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
y2 = −8x -
Find the equation of the tangent and normal to the circle x2+y2−6x+6y−8=0 at (2,2) .
-
Find centre and radius of the following circles.
x2+y2+6x−4y+4=0 -
-
Find the eccentricity of the ellipse with foci on x-axis if its latus rectum be equal to one half of its major axis.
-
Find centre and radius of the following circles.
x2+ (y+2)2 =0
-
-
Identify the type of the conic for the following equations:
(1) 16y2=−4x2+64
(2) x2+y2=−4x−y+4
(3) x2−2y=x+3
(4) 4x2−9y2−16x+18y−29 = 0 -
Find the equation of the parabola whose vertex is (5,-2) and focus(2,-2) .
-
Find the equation of the ellipse whose latus rectum is 5 and e= \(\frac { 2 }{ 3 } \)
-
Find the equation of the hyperbola with vertices (0,±4) and foci(0,±6).
-
-
Find the equations of tangent and normal to the ellipse x2+4y2=32 when \(\theta =\frac { \pi }{ 4 } \)
-
A circle of radius 3 units touches both the axes. Find the equations of all possible circles formed in the general form.
-
-
Find the equations of tangent and normal to the parabola x2+6x+4y+5=0 at (1,-3) .
-
Find the value of c if y = x + c is a tangent to the hyperbola 9x2 - 16y2 = 144.
-
A room 34m long is constructed to be a whispering gallery. The room has an elliptical ceiling, as shown in Fig. 5.64. If the maximum height of the ceiling is 8m, determine where the foci are located.
-
An equation of the elliptical part of an optical lens system is \(\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 } \) =1. The parabolic part of the system has a focus in common with the right focus of the ellipse .The vertex of the parabola is at the origin and the parabola opens to the right. Determine the equation of the parabola.
-
Find the equation of the parabola with vertex (-1,-2) , axis parallel to y -axis and passing through (3,6)
-
An equilateral triangle is inscribed in the parabola y2 = 4ax whose vertex is at the vertex of the parabola. Find the length of its side.
-
Find the equation of the ellipse whose eccentricity is \(\frac { 1 }{ 2 } \), one of the foci is(2,3) and a directrix is x = 7 . Also find the length of the major and minor axes of the ellipse.
-
A road bridge over an irrigation canal have two semi circular vents each with a span of 20m and the supporting pillars of width 2m. Use Fig.5.16 to write the equations that model the arches.
-
-
Two coast guard stations are located 600 km apart at points A(0,0) and B(0,600). A distress signal from a ship at P is received at slightly different times by two stations. It is determined that the ship is 200 km farther from station A than it is from station B. Determine the equation of hyperbola that passes through the location of the ship.
-
A kho-kho player In a practice session while running realises that the sum of tne distances from the two kho-kho poles from him is always 8m. Find the equation of the path traced by him of the distance between the poles is 6m.
-
-
Certain telescopes contain both parabolic mirror and a hyperbolic mirror. In the telescope shown in figure the parabola and hyperbola share focus F1 which is 14mabove the vertex of the parabola. The hyperbola’s second focus F2 is 2m above the parabola’s vertex. The vertex of the hyperbolic mirror is 1m below F1. Position a coordinate system with the origin at the centre of the hyperbola and with the foci on the y-axis. Then find the equation of the hyperbola.
-
A concrete bridge is designed as a parabolic arch. The road over bridge is 40m long and the maximum height of the arch is 15m. Write the equation of the parabolic arch.
-
The guides of a railway bridge is a parabola with its vertex at the highest point 15 m above the ends. If the span is 120 m, find the height of the bridge at 24 m from the middle point.
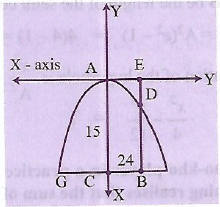
-
Find the foci, vertices and length of major and minor axis of the conic 4x2+36y2+40x−288y+532 = 0 .
