InstaQB

Home
Institutions
- Institutions
  
  Polytechnic Colleges
  
  Medical Colleges
  
  Arts & Science Colleges
  
  Universities
  
  Engineering Colleges
  
  Agricultural Colleges
  
  Research Institute
  
  Law Colleges
  
  Audiology and Speech Colleges
  
  Business & Management colleges
  
  Nursing colleges
  
  Hotel Management institutes
  
  Aeronautical Colleges
  
  Bachelor's Degree
Syllabus
Courses
Stateboard
- 12th Standard English Medium
  
  Maths
  
  Physics
  
  Chemistry
  
  Biology
  
  Computer Science
  
  Business Maths
  
  Economics
  
  Commerce
  
  Accountancy
  
  History
  
  Computer Applications
  
  Computer Technology
  12th Standard Tamil Medium
  
  உயிரியல்
  
  கணினி பயன்பாடுகள்
  
  கணினி அறிவியல்
  
  வணிகக் கணிதம்
  
  வணிகவியல்
  
  பொருளியல்
  
  கணிதவியல்
  
  வேதியியல்
  
  இயற்பியல்
  
  கணினி தொழில்நுட்பம்
  
  வரலாறு
  
  கணக்குப்பதிவியல்
  11th Standard English Medium
  
  Maths
  
  Commerce
  
  Economics
  
  Biology
  
  Business Maths
  
  Accountancy
  
  Computer Science
  
  Physics
  
  Chemistry
  
  Computer Applications
  
  History
  
  Computer Technology
  
  Bio - Zoology
  11th Standard Tamil Medium
  
  கணிதவியல்
  
  உயிரியல்
  
  பொருளியல்
  
  இயற்பியல்
  
  வேதியியல்
  
  வணிகக் கணிதம்
  
  கணினி அறிவியல்
  
  கணக்குப்பதிவியல்
  
  வணிகவியல்
  
  கணினி பயன்பாடுகள்
  10th Standard English Medium
  
  Mathematics
  
  Science
  
  Social Science
  
  9th Standard English Medium
  
  Mathematics
  
  Science
  
  Social Science
  
  8th Standard English Medium
  
  Mathematics
  
  Science
  
  Social Science
  7th Standard English Medium
  
  Mathematics
  
  Science
  
  Social Science
ICSE/ISC
- Class XII
  
  Mathematics
  
  Physics
  
  Accountancy
  
  Biology
  
  History
  
  Geography
  
  Psychology
  
  chemistry
  
  Economics
  
  Computer Science
  
  Political Science
  
  Business Studies
  Class XI
  
  Accountancy
  
  Chemistry
  
  Mathematics
  
  Biology
  
  Geography
  
  Physics
  
  History
CBSE
- 12Th Standard
  
  Physics
  
  Chemistry
  
  Maths
  
  Biology
  
  History
  
  Economics
  
  Commerce
  
  Geography
  
  Socialogy
  
  Business Studies
  
  Computer Science
  
  Biotechnology Class
  
  Political Science
  
  Home Science
  11Th Standard
  
  Physics
  
  Chemistry
  
  Maths
  
  Biology
  
  History
  
  Economics
  
  Commerce
  
  Socialogy
  
  Business Studies
  
  Geography
  
  Home Science
  
  Computer Science
  
  Biotechnology Class
  
  Political Science
  10Th Standard
  
  Physics
  
  Chemistry
  
  Biology
  
  Mathematics
  
  Economics
  
  Geography
  
  History & Civics
  
  Computer Application
  9Th Standard
  
  Physics
  
  Chemistry
  
  Biology
  
  mathematics
  
  Computer Application
  
  Economics
  
  Geography
  
  History & Civics

12th Maths Monthly Test - 2 ( Two Dimensional Analytical Geometry-II)

St. Britto Hr. Sec. School - Madurai

12th Maths Monthly Test - 2 ( Two Dimensional Analytical Geometry-II)-Aug 2020

Time : 2.30 Hours

Part - A

Generic 2 - Answer All Question

Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:
\(\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 } =1\)

Determine whether the points(-2,1),(0,0) and (-4,-3) lie outside, on or inside the circle
x²+y²−5x+2y−5=0 .

Find the eccentricity of the hyperbola. with foci on the x-axis if the length of its conjugate axis is \({ \left( \frac { 3 }{ 4 } \right) }^{ th }\) of the length of its tranverse axis.

Find centre and radius of the following circles.
x₂+ (y+2)² =0

If the line y = 3x + 1, touches the parabola y² = 4ax, find the length of the latus rectum?

Find the equation of the circle with centre (2,-1) and passing through the point (3,6) in
standard form.

Find the eccentricity of the ellipse with foci on x-axis if its latus rectum be equal to one half of its major axis.

Find the equations of the tangent and normal to hyperbola 12x²−9y²=108 at \(\theta =\frac { \pi }{ 3 } \) (Hint:
use parametric form)

Find the vertex, focus, equation of directrix and length of the latus rectum of the following:
x²−2x+8y+17=0

Obtain the equation of the circle for which (3,4) and (2,-7) are the ends of a diameter.

The line 3x+4y−12 = 0 meets the coordinate axes at A and B . Find the equation of the circle drawn on AB as diameter.

Find the equation of circles that touch both the axes and pass through (-4,-2) in general form.

If the equation3x²+(3−p)xy+qy²−2px =8pq represents a circle, find p and q . Also determine the centre and radius of the circle

Find centre and radius of the following circles.
x²+y²−x+2y−3= 0

Find the equation of tangent to the circle x² +y² + 2x - 3y - 8 = 0 at (2, 3).

A bridge has a parabolic arch that is 10m high in the centre and 30m wide at the bottom. Find the height of the arch 6m from the centre, on either sides.
Find the equation of the tangent and normal to the circle x²+y²−6x+6y−8=0 at (2,2) .

Find the vertex, focus, equation of directrix and length of the latus rectum of the following: y²−4y−8x+12=0

Find the equation of the parabola with vertex at the origin, passing through (2, -3) and symmetric about x-axis

Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:
\(\frac { { x }^{ 2 } }{ 25 } +\frac { { y }^{ 2 } }{ 144 } =1\)
Find the equation of the circle through the points (1,0),(-1,0) , and (0,1) .

Find the equation of the tangent at t = 2 to the parabolay² = 8x. (Hint: use parametric form)

Show that the absolute value of difference of the focal distances of any point P on the hyperbola is the length of its transverse axis.

Determine whether x+y−1=0 is the equation of a diameter of the circle x²+y²−6x+4y+c = 0 for all possible values of c .

Show that the linex−y+4=0 is a tangent to the ellipse x²+3y²=12 . Also find the coordinates
of the point of contact.

If a parabolic reflector is 24 cm in diameter and 6 cm deep, find its locus.

At a water fountain, water attains a maximum height of 4m at horizontal distance of 0.5 . m from its origin. If the path of water is a parabola, find the height of water at a horizontal distance of 0.75m from the point of origin.

Part - B

Generic 5 - Answer All Question

Find the equation of the ellipse whose eccentricity is \(\frac { 1 }{ 2 } \), one of the foci is(2,3) and a directrix is x = 7 . Also find the length of the major and minor axes of the ellipse.

A road bridge over an irrigation canal have two semi circular vents each with a span of 20m and the supporting pillars of width 2m. Use Fig.5.16 to write the equations that model the arches.

The foci of a hyperbola coincides with the foci of the ellipse \(\frac { { x }^{ 2 } }{ 25 } +\frac { y^{ 2 } }{ 9 } =1\). Find the equation of the hyperbola if its eccentricity is 2.

A kho-kho player In a practice session while running realises that the sum of tne distances from the two kho-kho poles from him is always 8m. Find the equation of the path traced by him of the distance between the poles is 6m.

Find the centre, foci, and eccentricity of the hyperbola 11x²−25y²−44x+50y−256 = 0

An equilateral triangle is inscribed in the parabola y² = 4ax whose vertex is at the vertex of the parabola. Find the length of its side.
For the ellipse4x²+y²+24x−2y+21 = 0 , find the centre, vertices, and the foci. Also prove that the length of latus rectum is 2 .

Find the vertex, focus, directrix, and length of the latus rectum of the parabola x²−4x−5y−1=0.

Certain telescopes contain both parabolic mirror and a hyperbolic mirror. In the telescope shown in figure the parabola and hyperbola share focus F₁ which is 14mabove the vertex of the parabola. The hyperbola’s second focus F₂ is 2m above the parabola’s vertex. The vertex of the hyperbolic mirror is 1m below F₁. Position a coordinate system with the origin at the centre of the hyperbola and with the foci on the y-axis. Then find the equation of the hyperbola.

The guides of a railway bridge is a parabola with its vertex at the highest point 15 m above the ends. If the span is 120 m, find the height of the bridge at 24 m from the middle point.

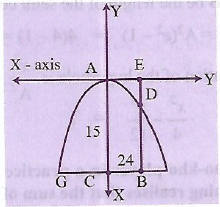
An arch is in the form of a parabola with its axis vertical. The arch is 10 m high and 5 m wide at the base. How wide is it 2 m from the vertex of the parabola?

Comment

Add Comment

Tamilnadu Stateboardszs - Class