St. Britto Hr. Sec. School - Madurai
12th Maths Monthly Test - 2 ( Probability Distributions)-Aug 2020
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Compute P(X = k)for the binomial distribution, B(n,p) where P(X = 10) = \(\begin{pmatrix} 10\\ 4\end{pmatrix}\)\(\begin{pmatrix} \frac{1}{5}\end{pmatrix}^4\)\(\begin{pmatrix}1- \frac{1}{5}\end{pmatrix}^{10-4}\)
-
Define Probability Density function
-
An urn contains 5 mangoes and 4 apples Three fruits are taken at randaom If the number of apples
taken is a random variable, then find the values of the random variable and number of points in its
inverse images. -
Prove that Var(x)=E(X2)-{E(X)]2
-
Prove that E(aX+b)=aE(X)+b
-
The probability density function of X is given by f(x) = \(\begin{cases}kxe^ {−2x}\quad forx > 0\\0\quad for x ≤ 0\end{cases}\)
-
Four bad oranges are accidentally mixed with sixteen good ones. Find the probability distribution of
bad oranges in a draw of two oranges. Also find the mean, variance and standard deviation of the
distribution. -
A box contains 4 red and 5 black marbles. Find the probability distribution of the red marbles in a
random draw of three marbles. Also find the mean and standard deviation of the distribution -
The p.d.f of a continuous random variable X is f(x) =
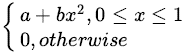 where a and b are some
where a and b are some
constants. Find(a) a and b if E(x) = \(\frac{3}{5}\)
(b) Var (X)
-
Suppose that a pair of fair dice are tossed and let random variable X denote the sum of outcomes.
Find the mean and variance of the probability distribution of X. -
The mean and variance of a binomial distribution are 4 and 2 respectively. Find the probability of at
least 6 success. -
The probability density function of random variable X is given by f(x) = \(\begin{cases} k \quad1 ≤ x ≤ 5\\0 \quad otherwise \end{cases}\)Find
(i) Distribution function
(ii) P(X < 3)
(iii) P(2 < X < 4)
(iv) P(3 ≤ X ) -
From a lot of 10 items containing 3 defective items, 4 items are drawn at random. Find the mean and
variance of the number of defective items drawn. -
The probability distribution of a random variable X is given by
X
0
1
2
3
P(X)
0.1
0.3
0.5
0.1
If Y=X2 +3X, find the mean and the variance of Y.
-
The probability density function random variable X is given by f(x) =\(\begin{cases} 16xe^{-4x} \quad for x > 0 \\0 \quad for x ≤ 0 \end{cases}\) find the
mean and variance of X. -
Ten coins are tossed simultaneously. What is the probability of getting (a) exactly 6 heads (b) at least
6 heads (c) at most 6 heads?
