St. Britto Hr. Sec. School - Madurai
12th Maths Monthly Test - 1( Two Dimensional Analytical Geometry-II)-Aug 2020
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:
\(\frac { { x }^{ 2 } }{ 3 } +\frac { { y }^{ 2 } }{ 10 } =1\) -
-
Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:
\(\frac { { x }^{ 2 } }{ 25 } +\frac { { y }^{ 2 } }{ 144 } =1\) -
Identify the type of conic section for the equation 3x2+2y2=14
-
-
-
On lighting a rocket cracker it gets projected in a parabolic path and reaches a maximum height of 4m when it is 6m away from the point of projection. Finally it reaches the ground 12m away from the starting point. Find the angle of projection.
-
A tunnel through a mountain for a four lane highway is to have a elliptical opening. The total width of the highway (not the opening) is to be 16m, and the height at the edge of the road must be sufficient for a truck 4m high to clear if the highest point of the opening is to be 5m approximately . How wide must the opening be?
-
-
Identify the type of conic and find centre, foci, vertices, and directrices of each of the following:
\(\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 } =1\) -
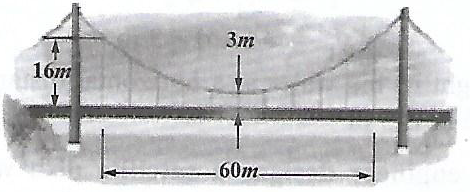
Parabolic cable of a 60m portion of the roadbed of a suspension bridge are positioned as shown below. Vertical Cables are to be spaced every 6m along this portion of the roadbed. Calculate the lengths of first two of these vertical cables from the vertex.
-
For the ellipse x2 + 3y2 = a2, find the length of major and minor axis.
-
Determine whether x+y−1=0 is the equation of a diameter of the circle x2+y2−6x+4y+c = 0 for all possible values of c .
-
Show that the linex−y+4=0 is a tangent to the ellipse x2+3y2=12 . Also find the coordinates
of the point of contact. -
Assume that water issuing from the end of a horizontal pipe, 7.5 m above the ground, describes a parabolic path. The vertex of the parabolic path is at the end of the pipe. At a position 2.5 m below the line of the pipe, the flow of water has curved outward 3m beyond the vertical line through the end of the pipe. How far beyond this vertical line will the water strike the ground?
-
Find the equation of tangent to the circle x2 +y2 + 2x - 3y - 8 = 0 at (2, 3).
-
A rod of length 1.2 m moves with its ends always touching the coordinate axes. The locus of a point P on the rod, which is 0.3 . m from the end in contact with x -axis is an ellipse. Find the eccentricity.
-
Find the equation of the circle through the points (1,0),(-1,0) , and (0,1) .
-
If a parabolic reflector is 24 cm in diameter and 6 cm deep, find its locus.
-
Find centre and radius of the following circles.
2x2+2y2−6x+4y+2=0 -
Find the equation of circles that touch both the axes and pass through (-4,-2) in general form.
-
Find the equations of the tangent and normal to the circle x2+y2=25 at P(-3,4).
-
-
Find the length of Latus rectum of the parabola y2 = 4ax .
-
Show that the line x + y + 1 = 0 touches the hyperbola \(\frac { { x }^{ 2 } }{ 16 } -\frac { { y }^{ 2 } }{ 15 } \) = 1 and find the co-ordinates of the point of contact
-
-
Find the equation of the hyperbola with vertices (0,±4) and foci(0,±6).
-
Find the area of th triangle found by the Unel Joining the vertex of the parabola x2 = -36y to the ends of the latus rectum.
-
-
A circle of radius 3 units touches both the axes. Find the equations of all possible circles formed in the general form.
-
Find the equation of the ellipse whose latus rectum is 5 and e= \(\frac { 2 }{ 3 } \)
-
-
The orbit of Halley’s Comet is an ellipse 36.18 astronomical units long and by 9.12 astronomical units wide. Find its eccentricity.
-
Find the condition for the line lx + my + n = 0 is Rtangent to the circle x2 + y2 = a2
-
Find the length of Latus rectum of the ellipse\(\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1\)
-
Find the equation of the parabola with vertex (-1,-2) , axis parallel to y -axis and passing through (3,6)
-
The parabolic communication antenna has a focus at 2m distance from the vertex of the antenna. Find the width of the antenna 3m from the vertex.
-
-
For the ellipse4x2+y2+24x−2y+21 = 0 , find the centre, vertices, and the foci. Also prove that the length of latus rectum is 2 .
-
A road bridge over an irrigation canal have two semi circular vents each with a span of 20m and the supporting pillars of width 2m. Use Fig.5.16 to write the equations that model the arches.
-
-
Find the centre, foci, and eccentricity of the hyperbola 11x2−25y2−44x+50y−256 = 0
-
Find the equation of the circle passing through the points(1,1), (2,-1) , and(3,2) .
-
The guides of a railway bridge is a parabola with its vertex at the highest point 15 m above the ends. If the span is 120 m, find the height of the bridge at 24 m from the middle point.
-
Find the equation of the ellipse whose eccentricity is \(\frac { 1 }{ 2 } \), one of the foci is(2,3) and a directrix is x = 7 . Also find the length of the major and minor axes of the ellipse.
