St. Britto Hr. Sec. School - Madurai
12th Maths Monthly Test - 1 ( Complex Numbers)-Aug 2020
-
-
-
-
-
If z=cos\(\frac { \pi }{ 4 } \)+i sin\(\frac { \pi }{ 6 } \), then
|z| =1, arg(z) =\(\frac { \pi }{ 4 } \)
|z| =1, arg(z) =\(\frac { \pi }{ 6 } \)
|z|=\(\frac { \sqrt { 3 } }{ 2 } \), arg(z)=\(\frac { 5\pi }{ 24 } \)
|z| =\(\frac { \sqrt { 3 } }{ 2 } \), arg (z) =tan-1\(\left( \frac { 1 }{ \sqrt { 2 } } \right) \)
-
The principal value of the amplitude of (1+i) is
\(\frac { \pi }{ 4 } \)
\(\frac { \pi }{ 12 } \)
\(\frac { 3\pi }{ 4 } \)
\(\pi \)
-
The complex number z which satisfies the condition \(\left| \frac { 1+z }{ 1-z } \right| \) =1 lies on
circle x2+y2 =1
x-axis
y-axis
the lines x+y=1
-
The value of (1+i)4 + (1-i)4 is
8
4
-8
-4
-
If \(z=\cfrac { \left( \sqrt { 3 } +i \right) ^{ 3 }\left( 3i+4 \right) ^{ 2 } }{ \left( 8+6i \right) ^{ 2 } } \) , then |z| is equal to
0
1
2
3
-
If \(\alpha \) and \(\beta \) are the roots of x2+x+1=0, then \({ \alpha }^{ 2020 }+{ \beta }^{ 2020 }\)
-2
-1
1
2
-
The conjugate of \(\frac { 1+2i }{ 1-(1-i)^{ 2 } } \) is _______
\(\frac { 1+2i }{ 1-(1-i)^{ 2 } } \)
\(\frac { 5 }{ 1-(1-i)^{ 2 } } \)
\(\frac { 1-2i }{ 1+(1+i)^{ 2 } } \)
\(\frac { 1+2i }{ 1+(1-i)^{ 2 } } \)
-
The value of \(\sum _{ i=1 }^{ 13 }{ \left( { i }^{ n }+i^{ n-1 } \right) } \) is
1+ i
i
1
0
-
If z = a + ib lies in quadrant then \(\frac { \bar { z } }{ z } \) also lies in the III quadrant if
a > b > 0
a < b < 0
b < a < 0
b > a > 0
-
If a = 1+ i, then a2 equals
1-i
2i
(1+i)(1-i)
i-1
-
If |z|=1, then the value of \(\cfrac { 1+z }{ 1+z } \) is
z
\(\bar { z } \)
\(\cfrac { 1 }{ 2 } \)
1
-
If z1,z2, and z3 are three complex numbers such that |z1|=1,|z2|=2|z3|=3 and |z1+z2+z3|=1,show that |9z1z2+4z1z2+z2z3|=6
-
Write in polar form of the following complex numbers
\(3-i\sqrt { 3 } \) -
Prove the following properties
\(Ro\left( z \right) =\cfrac { z+\bar { z } }{ 2 } \) and Im\(\left( z \right) =\cfrac { z-\bar { z } }{ 2i } \) -
Show that the equation \({ z }^{ 3 }+2\bar { z } =0\) has five solutions
-
-
Obtain the Cartesian form of the locus of z=x+iy in each of the following cases
\(\overline { z } =2^{ -1 }\). -
Evaluate the following if z=5−2i and w= −1+3i
z−iw
-
-
Find the modulus and principal argument of the following complex numbers.
\(\sqrt { 3 } \)-i
-
If z1=3,z2=-7i, and z3=5+4i, show that z1(z2+z3)=z1z2+z1z3
-
Simplify the following:
\(\sum _{ n=1 }^{ 102 }{ { i }^{ n } } \)
-
If (cosθ + i sinθ)2 = x + iy, then show that x2+y2 =1
-
Find the modulus of the following complex numbers
\(\cfrac { 2i }{ 3+4i } \) -
Find the modulus and principal argument of the following complex numbers.
\(-\sqrt { 3 } +i\)
-
-
If z=2−2i, find the rotation of z by θ radians in the counter clockwise direction about the origin when \(\theta =\cfrac { 3\pi }{ 2 } \).
-
If \(\cfrac { 1+z }{ 1-z } =cos2\theta +isin2\theta \), show that z=itan\(\theta\)
-
-
It z1 and z2 are two complex numbers, such that |z1| = Iz2|, then is it necessary that z1 = z2?
-
If z =1, show that \(2\le \left| { z }^{ 2 }-3 \right| \le 4\)
-
Obtain the Cartesian form of the locus of z=x+iy in each of the following cases
\(\left[ Re\left( iz \right) \right] ^{ 2 }=3\)
-
If z = (cosθ + isinθ), show that zn + \(\frac { 1 }{ { z }^{ n } } \) = 2cosnθ and zn − \(\frac { 1 }{ { z }^{ n } } \) = 2isinnθ
-
-
If z1,z2 and z3 ,are complex numbers such that |z1|=|z2|=|z3|=|z1+z2+z3|=1 find the value of \(\left| \cfrac { 1 }{ { z }_{ 1 } } +\cfrac { 1 }{ z_{ 2 } } +\cfrac { 1 }{ { z }_{ 3 } } \right| \)
-
Find the quotient \(\cfrac { 2\left( cos\cfrac { 9\pi }{ 4 } +isin\cfrac { 9\pi }{ 4 } \right) }{ 4\left( cos\left( \cfrac { -3\pi }{ 2 } + \right) isin\left( \cfrac { -3\pi }{ 2 } \right) \right) } \) in rectangular form
-
-
Prove the following properties
Ro(z) = \(\frac { z+\overline { z } }{ 2 } \) and Im(z) = \(\frac { z-\overline { z } }{ 2i } \)
-
Simplify \(\left( sin\frac { \pi }{ 6 } +icos\frac { \pi }{ 6 } \right) ^{ 18 }\)
-
Show that the complex numbers 3 + 2i, 5i, -3 + 2i and -i form a square.
-
Show that the points \(1,\frac { -1 }{ 2 } +i\frac { \sqrt { 3 } }{ 2 } ,and\frac { -1 }{ 2 } -i\frac { \sqrt { 3 } }{ 2 } \) are the vertices of an equilateral triangle.
-
-
Simplify the following:
i1729
-
If z=2−2i, find the rotation of z by θ radians in the counter clockwise direction about the origin
whenθ = \(\frac { 2\pi }{ 3 } \)
-
-
Evaluate the following if z=5−2i and w= −1+3i
(z+w)2 -
Find the circle roots of -27.
-
If the complex number 2 + i and 1-2i are equidistant from x + iy then show that x+3y = 0.
-
-
Solve the equation z3+8i=0,where
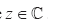
-
If z1 ,z2 and z3 are three complex numbers such that |z1 |=1,|z2 |=2|z3 |=3 and |z1 +z2 +z3 |=1,show
that |9z1 z2 +4z1 z2 +z2 z3 |=6
-
-
Show that \(\left( \frac { i+\sqrt { 3 } }{ -i+\sqrt { 3 } } \right) ^{ 2\omega }+\left( \frac { i-\sqrt { 3 } }{ i+\sqrt { 3 } } \right) ^{ 2\omega }\)=-1
-
Solve the equation z +8i=0,where Z \(\in \) C
-
If 2cosa = x + \(\frac { 1 }{ x } \) and 2cosβ = y + \(\frac { 1 }{ y } \) show that
i) \(\frac { x }{ y } +\frac { y }{ x } \) = 2cos(α − β).
ii) \(xy-\frac { 1 }{ xy } \) = 2isin(α + β)
iii) \(\frac { { x }^{ m } }{ { y }^{ n } } -\frac { { y }^{ n } }{ { x }^{ m } } \) = 2isin(mα − nβ)
iv) \({ x }^{ m }{ y }^{ n }+\frac { 1 }{ { x }^{ m }{ y }^{ n } } \) = 2cos(mα + nβ)
-
Find all cube roots of \(\sqrt { 3 } +i\)
