St. Britto Hr. Sec. School - Madurai
12th Business Maths Model Exam -1-Aug 2020
-
-
The starting annual salaries of newly qualified chartered accountants (CA's) in South Africa follow a normal distribution with a mean of Rs.1,80,000 and a standard deviation of Rs.10,000. What is the probability that a randomly selected newly qualified CA will earn between Rs.1,65,000 and Rs.1,75,000 per annum?
0.819
0.242
0.286
0.533
-
Given E(X) = 5 and E(Y) = -2, then E(X – Y) is
3
5
7
-
Area bounded by the curve y = \(\frac{1}{x}\) between the limits 1 and 2 is
log2 sq.units
log5 sq.units
log3 sq.units
log 4 sq.units
-
ഽ2xdx is
2x log 2 + c
2x + c
\(\frac { 2^{ x } }{ log2 } +c\)
\(\frac { log2 }{ { 2 }^{ x } } +c\)
-
For the system of equations x+2y+3z=1, 2x+y+3z=25x+5y+9z =4
there is only one solution
there exists infinitely many solutions
there is no solution
None of these
-
A finite subset of statistical individuals in a population is called __________
a sample
a population
universe
census
-
The quantities that can be numerically measured can be plotted on a
p - chart
c – chart
x bar chart
np – chart
-
E[X-E(X)] is equal to
E(X)
V(X)
0
E(X) - X
-
A ________ is a statement or an assertion about the population parameter.
hypothesis
statistic
sample
census
-
-
A homogeneous differential equation of the form \(\frac { dy }{ dx } \) = f\(\left( \frac { y }{ x } \right) \) can be solved by making substitution,
y = v x
v = y x
x = v y
x = v
-
Monthly expenditure on their credit cards, by credit card holders from a certain bank, follows a normal distribution with a mean of Rs.1,295.00 and a standard deviation of Rs.750.00. What proportion of credit card holders spend more than Rs.1,500.00 on their credit cards per month?
0.487
0.392
0.500
0.791
-
-
If c is a constant, then E(c) is
0
1
cfc
c
-
-
Area bounded by the curve y = x (4 − x) between the limits 0 and 4 with x − axis is
\(\frac{30}{3}\) sq.units
\(\frac{31}{3}\)sq.units
\(\frac{32}{3}\) sq.units
\(\frac{15}{2}\) sq.units
-
A formula or equation used to represent the probability distribution of a continuous random variable is called
probability distribution
distribution function
probability density function
mathematical expectation
-
-
The probability that a standard normal variate z will be
A B 1) Greater than 1.09 a) 0.8163 2) less than - 1.65 b) .1379 3) lying between - 1.00 and 1.96 c) 0.0495 4) lying between 1.25 and 2.75 d) 0.1026 The correct match is
1 - a, 2 - b, 3 - c, 4 - d
1 - d, 2 - c, 3 - a, 4 - b
1 - d, 2 - a, 3 - c, 4 - b
1 - b, 2 - c, 3 - a, 4 - d
-
A homogeneous differential equation of the form \(\frac { dy }{ dx } \) = f\(\left( \frac { x }{ y } \right) \) can be solved by making substitution,
x = v y
y = v x
y = v
x = v
-
If f (x) is a continuous function and a < c < b ,then \(\int _{ a }^{ c }{ f(x) } dx+\int _{ c }^{ b }{ f(x) } dx\) is
\(\int _{ a }^{ b }{ f(x) } dx+\int _{ a }^{ c }{ f(x) } dx\)
\(\int _{ a }^{ c }{ f(x) } dx+\int _{ a }^{ b }{ f(x) } dx\)
\(\int _{ a }^{ b }{ f(x) } dx\)
0
-
North-West Corner refers to ________
top left corner
top right corner
bottom right corner
bottom left corner
-
From the following table obtain a polynomial of degree y in x
x 1 2 3 4 5 y 1 -1 1 -1 1 -
A sample of 100 students are drawn from a school. The mean weight and variance of the sample are 67.45 kg and 9 kg. respectively. Find
(a) 95% and
(b) 99% confidence intervals for estimating the mean weight of the students. -
Explain Factor Reversal Test.
-
Assuming that a fatal accident in a factory during the year is 1/1200, calculate the probability that in a factory employing 300 workers there will be atleast two fatal accidents in a year. (given e-0.25 = 0.7788).
-
-
The marginal cost of production of a firm is given by C'(x) = 5 + 0.13x , the marginal revenue is given by R'(x) = 18 and the fixed cost is Rs. 120. Find the profit function.
-
The distribution of a continuous random variable X in range (–3, 3) is given by p.d.f.
f(x)={\(\frac { 1 }{ 16 } (3+{ x) }^{ 2 },\quad -3\le x\le -1\\ \frac { 1 }{ 16 } { (6-2x) }^{ 2 },-1\le x\le 1\\ \frac { 1 }{ 16 } { (3-x) }^{ 2 },1\le x\le 3\)
Verify that the area under the curve is unity.
-
-
Integrate the following with respect to x.
sin3 x -
What is the difference between Assignment Problem and Transportation Problem?
-
In a photographic process, the developing time of prints may be looked upon as a random variable having the normal distribution with a mean of 16.28 seconds and a standard deviation of 0.12 second. Find the probability
that it will take less than 16.35 seconds to develop prints. -
A discrete random variable. X has the following probability distribution
X 0 1 2 3 4 5 6 7 8 P (X) a 3a 5a 7a 9a 11a 13a 15a 17a Find the value of a and P(X < 3)
-
The population of a city in a censes taken once in 10 years is given below. Estimate
the population in the year 1955.Year 1951 1961 1971 1981 Population in lakhs 35 42 58 84 -
The birth weight of babies is normally distributed with mean 3,500 g and standard deViation 500 g. What is the probability that a baby is born that weighs less than 3,100 g?
-
Integrate the following with respect to x.
xn log x -
Using second fundamental theorem, evaluate the following:
\(\int _{ 0 }^{ 3 }{ \frac { { e }^{ x }dx }{ 1+{ e }^{ x } } } \) -
Integrate the following with respect to x.
x8(1+x9)5 -
Suppose, the life in hours of a radio tube has the following p.d.f
f(x)=\(\frac { 100 }{ { x }^{ 2 } } ,when\quad \ge 100\\ 0,\quad when\quad x<100\)
Find the distribution function. -
The following data gives readings of 10 samples of size 6 each in the production of a certain product. Draw control chart for mean and range with its control limits.
Sample 1 2 3 4 5 6 7 8 9 10 Mean 383 508 505 582 557 337 514 614 707 753 Range 95 128 100 91 68 65 148 28 37 80 -
A die is thrown 120 times and getting 1 or 5 is considered a success. Find the mean and variance of the number of successes.
-
A continuous random variable X has the following p.d.f
f(x)=ax, 0\(\le\)x\(\le\)1
Determine the constant a and also find P\(\\ \left[ X\le \frac { 1 }{ 2 } \right] \) -
The following data gives the readings for 8 samples of size 6 each in the production of a certain product. Find the control limits using mean chart.
Sample 1 2 3 4 5 6 Mean 300 342 351 319 326 333 Range 25 37 20 28 30 22 Given for n = 6, A2 = 0.483,
-
In tossing of a five fair coin, find the chance of getting exactly 3 heads.
-
Find the sample size for the given standard deviation 10 and the standard error with respect of sample mean is 3.
-
Consider the following pay-off (profit) matrix Action States
Action States (s1) (s2) (s3) (s4) A1 5 10 18 25 A2 8 7 8 23 A3 21 18 12 21 A4 30 22 19 15 Determine best action using maximin principle.
-
If a random variable X follows Poisson distribution such that P(X = 2) = 9. P(X = 4) + 90 P(X = 6) then find the mean and variance.
-
Find the initial basic feasible solution for the following transportation problem by VAM

-
Determine the mean and variance of a discrete random variable, given its distribution as follows.
X=x 1 2 3 4 5 6 Fx(x) \(\frac{1}{6}\) \(\frac{2}{6}\) \(\frac{3}{6}\) \(\frac{4}{6}\) \(\frac{5}{6}\) 1 -
the Laspeyre’s, Paasche’s and Fisher’s price index number for the following data. Interpret on the data.
Commodities Price Quandity 2000 2010 2000 2010 Rice 38 35 6 7 Wheat 12 18 7 10 Rent 10 15 10 15 Fuel 25 30 12 16 Miscellaneous 30 33 8 10 -
The probability distribution of the discrete random variables X and Y are given below.
X 0 1 2 3 P(X) \(\frac { 1 }{ 5 } \) \(\frac { 2 }{ 5 } \) \(\frac { 1 }{ 5 } \) \(\frac { 1 }{ 5 } \) Y 0 1 2 3 P(Y) \(\frac { 1 }{ 5 } \) \(\frac{3}{10}\) \(\frac { 2 }{ 5 } \) \(\frac{1}{10}\) Prove that E(Y2) = 2 E(X).
-
Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.
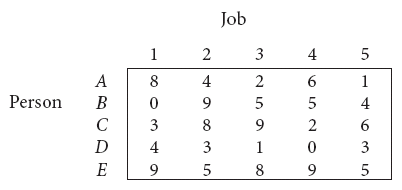
-
Calculate the cost of living index number by consumer price index number for the year 2016 with respect to base year 2011 of the following data.
Commodities Price Quantity Base year Current year Rice 32 48 25 Sugar 25 42 10 Oil 54 85 6 Coffe 250 460 1 Tea 175 275 2
