MABS Institution
11th Physics Monthly Test - 1 ( Waves )-Aug 2020
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
Give the relation between velocity v, angular frequency \(\omega\) and wave number \(\lambda\)?
-
What is meant by reverberation time?
-
What is the effect of pressure on velocity of sound in gas?
-
How can we distinguish experimentally between longitudinal and transverse waves?
-
Consider a tuning fork which is used to produce resonance in an air column. A resonance air column is a glass tube whose length can be adjusted by a variable piston. At room temperature, the two successive resonances observed are at 20 cm and 85 cm of the column length. If the frequency of the length is 256 Hz, compute the velocity of the sound in air at room temperature.
-
A baby cries on seeing a dog and the cry is detected at a distance of 3.0 m such that the intensity of sound at this distance is 10-2 W m-2. Calculate the intensity of the baby’s cry at a distance 6.0 m.
-
Check the dimensional of the wave y = sin(x−vt). If it is dimensionally wrong, write the above equation in the correct form
-
An observer observes two moving trains, one reaching the station and other leaving the station with equal speeds of 8 m s−1. If each train sounds its whistles with frequency 240 Hz, then calculate the number of beats heard by the observer.
-
Derive the Equation of a plane progressive wave.
-
-
Calculate the velocity of the travelling pulse as shown in the figure below. The linear mass density of pulse is 0.25 kg m-1. Further, compute the time taken by the travelling pulse to cover a distance of 30 cm on the string.

-
Two vibrating tuning forks produce waves whose equation is given by y1 = 5 sin(240\(\pi\)t) and y2 = 4 sin(244πt). Compute the number of beats per second.
-
-
Consider a string whose one end is attached to a wall. Then compute the following in both situations given in figure (assume waves crosses the distance in one second)
(a) Wavelength, (b) Frequency and
(c) Velocity -
Describe the formation of beats.
-
Write the characteristics of wave motion.
-
Briefly explain the difference between travelling waves and standing waves.
-
Consider two sources A and B as shown in the figure below. Let the two sources emit simple harmonic waves of same frequency but of different amplitudes, and both are in phase (same phase). Let O be any point equidistant from A and B as shown in the figure. Calculate the intensity at points O, Y and X. (X and Y are not equidistant from A & B)
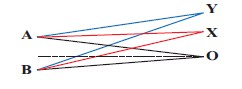
-
Show that the velocity of a travelling wave produced in a string is v\(\sqrt { \frac { T }{ \mu } } \)
-
Write the applications of reflection of sound waves.
-
How does the wave y = sin(x − a) for a = 0, a=\(\frac { \pi }{ 4 } ,a=\frac { \pi }{ 2 } ,a=\frac { 3\pi }{ 2 } \)and a = \(\pi\) look like?. Sketch this wave.
-
-
Let the source propagate a sound wave whose intensity at a point (initially) be I. Suppose we consider a case when the amplitude of the sound wave is doubled and the frequency is reduced to one-fourth. Calculate now the new intensity of sound at the same point ?.
-
Explain the concepts of fundamental frequency, harmonics and overtones in detail.
-
-
Write Characteristics of progressive waves
-
What is meant by Doppler effect?.
Discuss the following cases
(1) Source in motion and Observer at rest
(a) Source moves towards observer
(b) Source moves away from the observer
(2) Observer in motion and Source at rest.
(a) Observer moves towards Source
(b) Observer resides away from the Source
(3) Both are in motion
(a) Source and Observer approach each other
(b) Source and Observer resides from each other
(c) Source chases Observer
(d) Observer chases Source -
Describe Newton’s formula for velocity of sound waves in air and also discuss the Laplace’s correction.
