MABS Institution
11th Physics Monthly Test - 1 (Kinematics)-Aug 2020
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
A boy is running on a circular track of radius 50 m. Calculate the displacement of the boy after completing 5 rounds of the track.
-
Distinguish between uniformly accelerated and non-uniformly accelerated motion.
-
A car is moving along X-axis. As shown in figure it moves from O to P in 18 seconds and return from P to Q in 6 second. What are the average velocity and average speed of the car in going from
(I)O to P
(II) From O to P and back to Q

-
Define unit radian.
-
A bus travels 6 km towards north at an angle of 45o to the east and then travels 4 km towards north at an angle of 135o to the east. How far is its final position, due east and due north? How far is the point from the starting point? What angle does the straight line joining its initial and final position makes with the east?
-
The velocity-time graph for a vehicle is shown in the figure. Draw acceleration-time graph from it.
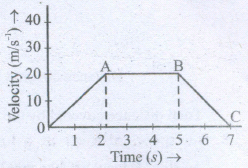
-
At what angle do the two forces (P + Q) and (P - Q) act so that the resultant is \(\sqrt { { 3P }^{ 2 }+Q^{ 2 } } \)
-
A projectile is fired horizontally with a velocity u making an angle θ. Derive the expression for time of the flight.
-
A swimmer's speed in the direction of flow of a river is 12 km h-1. Against the direction of flow ofthe river the swimmer's speed is 6 km h-1.Calculate the swimmer's speed in still water and the velocity of the river flow.
-
-
Two vectors \(\vec A\) and \(\vec B\) are given in the component form as \(\overrightarrow { A } =5\hat { i } +7\hat { j } -4\hat { k } \) and \(\overrightarrow { B } =6\hat { i } +3\hat { j } +2\hat { k } \). Find \(\vec { A } +\vec { B } ,\vec { B } +\vec { A } ,\vec { A } -\vec { B } ,\vec { B } -\vec { A } \)
-
An object is in uniform motion along a straight line, what will be position time graph for the motion of object, if (i) X0 = positive, v = negative is constant.
(i) x0 = positive v negative is \(\left| \overrightarrow { v } \right| \)constnat
(ii) both X0 and v are negative Ivl is constant.
(iii) X0 = negative, v = positive \(\left| \overrightarrow { v } \right| \)is constant.
(iv) both X0 and v are positive \(\left| \overrightarrow { v } \right| \) is constant where x0is position at t = 0
-
-
Derive the expression for a body projected horizontally?
-
A bomb is dropped from an aeroplane when it is directly above a target at a height of 1000m. The aeroplane is moving horizontally with a speed of 500 kmh-1. By how much distance will the bomb miss the target?
-
Find the distance travelled by the particle during the time t = 0 to t = 3 seconds from the figure.
-
Discuss the properties of scalar and vector products.
-
Explain in details the subtraction of two vectors.
-
A train moving with a speed of 100 km/h can be stopped by brakes after atleast 15m. What will be the minimum stopping distance, if the same train is moving at a speed of 120 km/h?
-
Two particles move along x axis. The position of particle is given by x = 6.0 t2 + 4.0 t + 2.0, acceleration of particle 2 is given by a = -6.0 t and t =0, its velocity is 30 ms-1, When the velocities of the particles match, find their velocities.
-
Two bodies of mass 30 and 6g have position vectors \(2\hat { i } +\hat { j } +3k\quad and\quad \hat { j } +3\hat { j } +2k\) respectively. Find the position vectors of centre of mass.
-
The velocity time graph of a particle is given by
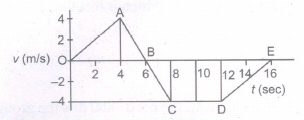
(i) Calculate distance and displacement of particle from given v-t graph.
(ii) Specify the time for which particle undergone acceleration, retardation and moves with constant velocity.
(iii) Calculate acceleration, retardation from given v-t graph.
(iv) Draw acceleration-time graph of given v-t graph. -
-
Define the term motion and explain the different types of motion.
-
Explain the types of motion with example.
-
-
Write note on integration.
-
Derive the kinematic equations of motion for constant acceleration. (OR) Derive equations of uniformly accelerated motion by calculus method.
